In the subject of geometry, a figure which is created by two rays or lines that share a common fixed point is called an angle. The word “angle” is obtained from the Latin word “angulus”, which means a corner. The two rays of the angle are called the sides of the angle, and the common fixed point is called the vertex. In case if the angles are created by the intersection of two planes in the Euclidean or any different space, the angles are then named dihedral angles. The angle is expressed by the symbol “∠”. The angle measurement between the two rays can be symbolized by the Greek letter θ, α, β, etc. If the angles are measured from a line, we can see two different types of angles, such as a positive and a negative angle.
Supplementary Angles
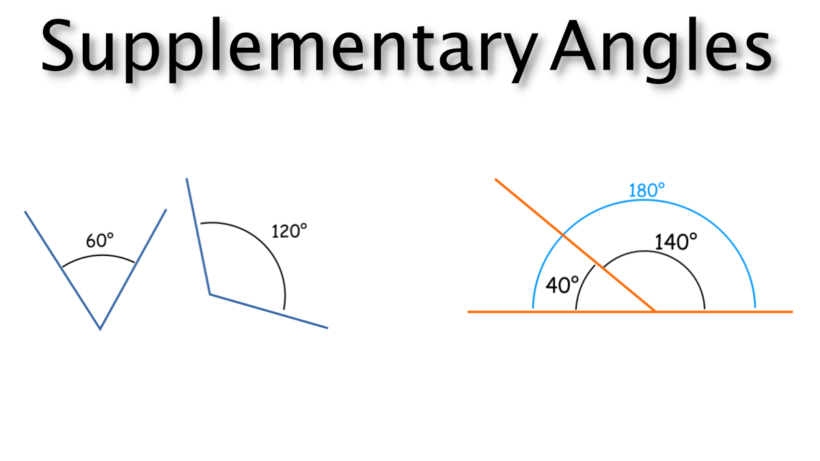
The word supplementary is obtained from two Latin words “supplere” and “plere”. Where “supplere” means supply, and “plere” means fill. Consecutively, supplementary means something when supplied to complete a thing. Thus, supplementary angles are a pair of two angles forming a straight angle that is 180 degrees, when they are put together. These two angles are then proved as supplements of each other.
What are Supplementary Angles?
Two angles are known to be supplementary angles if their sum adds up to 180 degrees. Supplementary angles always form a straight angle that is 180 degrees, when they are put together. In easy words, angle A and angle B are supplementary to each other, then Angle A + Angle B = 180o. In this scenario, Angle A and Angle B are called “supplements” of each other.
Types of Supplementary Angles
Supplementary angles can either be adjacent or nonadjacent in nature. So, there are two kinds of supplementary angles. The two types of supplementary angles are expressed below.
- Adjacent supplementary angles
- Non-adjacent supplementary angles
Adjacent Supplementary Angles
Two supplementary angles having a common vertex and a common arm are proved to be adjacent supplementary angles.
Non-adjacent Supplementary Angles
Two supplementary angles that are not adjacent to each other are proved to be non-adjacent supplementary angles.
Supplementary vs Complementary Angles
The supplementary and complementary angles are the angles that always appear in a pair, summing up to 180 and 90 degrees respectively, and have various real-time applications, the most common example being the crossroads. Let’s have a look at the differences between them supplementary and complementary. Here is a tip for the students to understand the difference between supplementary angles and complementary angles.
- Here “S” is for “Supplementary” and “S” is for the straight line. Hence, you can remember that two when supplementary angles are put together form a straight angle.
- “C” is used for “Complementary” and even for the corner. Hence, the students can remember that two complementary angles when arranged together form a corner or right angle.
Properties of Supplementary Angles
The essential and primary properties of supplementary angles are given below:
- The two angles are proved to be supplementary angles only when they add up to 180 degrees.
- The two angles together make a straight line, but the angles do not have to be together.
- “S” of supplementary angle stands for the “Straight” line. This means they form 180 degrees.
Supplementary Angles Theorem
The supplementary angle theorem states and explains that if any two given angles are supplementary to the same angle, then the two angles are proved to be congruent.
Conclusion
Supplementary and are very important concepts in mathematics and geometry. Complementary angles. Supplementary angles can also be very confusing for children. The world of the internet has made everything very easy and accessible for students. Supplementary angles can easily be understood with the help of online worksheets and courses that make it very interesting for students to understand and grasp.
Laila Azzahra is a professional writer and blogger that loves to write about technology, business, entertainment, science, and health.